Theorem 9.3 Class 9 Maths Explanation with Proof

Today, we will discuss theorem 9.3 class 9 Maths which is related to Chapter 9 Areas of Parallelograms and Triangles  Class 9 Mathematics. After understanding theorem 9.3, you can solve the exercise questions given in the NCERT book of Class 9 Maths.

 Theorem 9.3 Class 9

Two triangles having the same base (or equal bases) and equal areas lie between the same parallels.

Given 

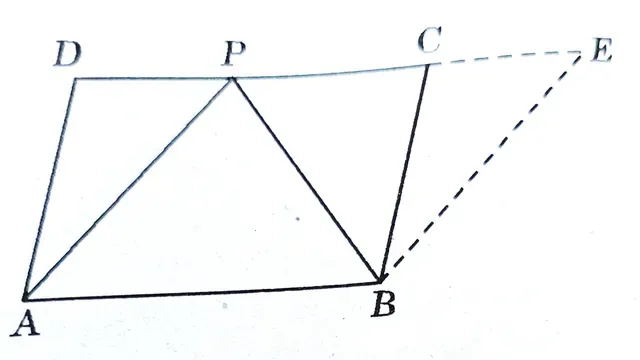
A triangle APB and a ||gm ABCD lie on the same base AB and between the same parallels AB and DC.

To Prove

`ar(∆ABP)=frac{1}{2} ar(ABCD)`

Construction 

Draw BE || AP to meet DC produced at E to obtain another parallelogram ABEP.

Proof 

We know that parallelograms on the same base and between the same parallels are equal in area.

ar(ABEP)=ar(ABCD)

[||gm lying on same base AB and between same parallels AB and DE ]

∆ABP≅∆EPB (∵diagonal BP divides ||gm ABEP into two  congruent triangles)

⇒ar(ABP)=ar(EPB) ………….(ii)

But,  ar(ABP)+ar(EPB)=ar(ABEP)

⟹ar(ABP)+ar(ABP)=ar(ABEP) 

2ar(ABP)=ar(ABEP)

ar(ABP)=1/2 ar(ABEP) …………..(iii)

Thus we have `ar(ABP)=frac{1}{2} ar(ABCD)` from(iii) and (i)

Hence proved

Related Topics

1. Theorem 9.1

2. Theorem 9.2