Theorem 10.7 Class 9 Maths Explanation with Proof

 Today, we will discuss theorem 10.7 class 9 Maths which is related to Chapter 10 Circles Class 9 Mathematics. After understanding theorem 10.7, you can solve the exercise questions given in the NCERT book of Class 9 Maths.

 Theorem 10.7 Class 9

Chords equidistant from the centre of a circle are equal in length.

Given 

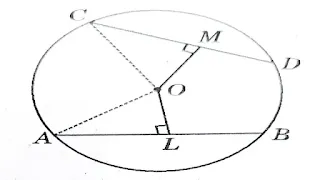
Two chords AB and CD of a circle C(O,r) which are equidistant from its centre i.e. OL=OM,

Where OL⊥AB and OM⊥CD.

To Prove 

Chords  are equal i.e. AB=CD

Construction 

Join OA and OC.

Proof 

Since the perpendicular from the centre to a chord bisects the chord.

Therefore   OL⊥AB      ⇒AL=BL

   ⇒   `AL=frac{1}{2} AB` …………………..(i)

And   OM⊥CD

⇒    CM=DM 

⇒     `CM=frac{1}{2} CD` ……………………(ii)

In triangles OAL and OCM, we have

OA=OC(each equal to the radius of the circle)

∠OLA=∠OMC (each equal to 90°)

And  OL=OM(given)

 ∴By RHS criterion of congruency, we have

∆OAL=∆OCM 

⇒AL=CM 

⇒`frac{1}{2} AB=frac{1}{2} CD` (using equations (i) and (ii))

⇒AB=CD 

Hence the chords of a circle which are equidistant from the centre are equal.

Hence proved

 Related Topics

1. Theorem 10.8

2. Theorem 10.6