NCERT Solutions of Quadrilaterals for Class 9

Today we will discuss the NCERT solution of quadrilaterals for class 9 in which you will learn important definitions of quadrilaterals and theorems, and exercise solutions of chapter 8 class 9 Maths.

Important Definitions related to Quadrilaterals

Quadrilateral

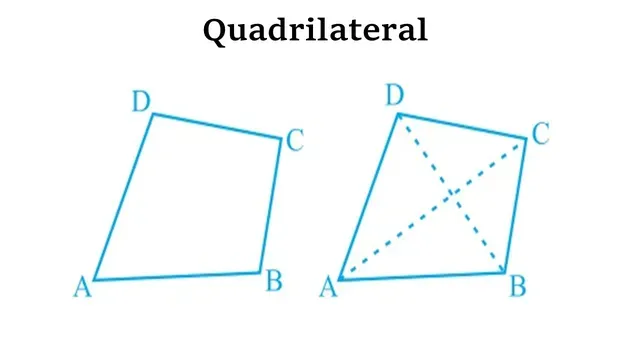
1. Quadrilateral – A plane figure bounded by four-line segments is called a quadrilateral. For example, the following is a quadrilateral ABCD where AB, BC, CD, and DA are four sides and  ∠A,∠B,∠C, and ∠D  are four angles.

2. Vertex – The points of intersection of sides are known as vertices. Here A, B, C, and D are four vertices of the quadrilateral.

3. Diagonal – A line joining opposite vertices is called a diagonal. Here AC and BD are the diagonals of quadrilateral ABCD.

4. Consecutive or adjacent sides – Two sides of a quadrilateral are consecutive or adjacent sides if they have a common point. Here AB, BC, CD, AD.

5. Opposite sides-  Two sides of a quadrilateral are opposite sides if they have no common endpoint.

6. Consecutive or adjacent angles-  Two angles of a quadrilateral are consecutive or adjacent angles if their common arm is a side of the quadrilateral. For example,  ∠A and ∠B are adjacent angles.

7. Opposite sides-  Two angels of a quadrilateral are said to be opposite angels if they do not have a common arm. For example, angles  ∠A and ∠C  are two adjacent angles.

8. Sum of all four angles of a quadrilateral is 4 right angles(360°).

9. Types of Quadrilaterals

Kite – A quadrilateral whose two pairs of adjacent sides are equal is known as a kite.

Trapezium – A quadrilateral whose one pair of opposite sides is known as a trapezium.

Parallelogram – A quadrilateral whose two pairs of opposite sides are parallel and equal is known as a parallelogram. A parallelogram is also a trapezium but a trapezium is not a parallelogram.

Rectangle –  A quadrilateral whose opposite sides are parallel and equal and also each angle is 90° is known as a rectangle. A rectangle is also a parallelogram but a parallelogram is not necessarily a rectangle.

Rhombus -  A special parallelogram whose each side is equal is known as a rhombus.

Square – A special parallelogram whose all sides are equal and each angle is 90° is known as a square.

10. Note that a square, rectangle, and rhombus are all parallelograms.

i. A square is a rectangle and also a rhombus.

ii. A parallelogram is a trapezium.

iii. A kite is not a parallelogram.

iv. A trapezium is not a parallelogram (as only one pair of opposite sides is parallel in a trapezium and we require both pairs to be parallel in a parallelogram).

v. A rectangle or a rhombus is not a square.

Related Topics 

1. Theorem 8.1

2. Theorem 8.2