Theorem 6.4 Class 10 Maths Explanation with Proof

In this post, we will discuss theorem 6.4 Class 10 Maths which is related to Chapter 6 Triangles Class 10 Mathematics. After understanding theorem 6.4, you can solve the exercise questions given in the NCERT book of Class 10 Maths.

 

 Theorem 6.4 Class 10 Proof

(SSS similarity criterion)

If in two triangles, the sides of one triangle are proportional to(i.e., in the same ratio of ) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similar.

Given 

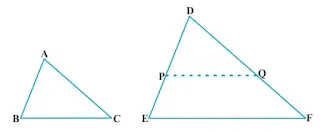
 Two triangles ∆ABC and ∆DEF such that

`frac{AB}{DE}=frac{BC]{EF}=frac{AC]{DF}` 

To prove 

∆ABC ~∆DEF 

Construction 

Let us take ∆ABC and ∆DEF such that

`frac{AB}{DE}=frac{BC}{EF}=frac{AC]{DF}` (<1)

Cut DP=AB and DQ=AC. Join PQ

Proof 

`frac{AB}{DE}=frac{AC}{DF}` 

⟹`frac{DP}{DE}=frac{DQ]{DF}` [∵AB=DP and AC=DQ]

⟹PQ∥EF 

∴ ∠P=∠E(by converse of BPT)……………(i)

And ∠Q=∠F()……………(ii)

  ⟹`frac{DP}{DE}=frac{PQ}{EF}` 

  ⟹`frac{AB}{DE}=frac{PQ}{EF}` [∵DP=AB]……….(iii)

But    `frac{AB}{DE}=frac{BC}{EF}` (given)……….(iv)

From (iii) and (iv), we get

   `frac{PQ}{EF}=frac{BC}{EF}` 

  ⟹BC=PQ 

AB=DP and AC=DQ     (by construction)

Thus AB=DP, AC=DQ, BC=PQ

∴∆ABC≅∆DPQ           [by SSS congruence]

∴∠A=∠D,∠B=∠P,∠C=∠Q    [by CPCT]

But ∠P=∠E

∴∠Q=∠F [from(i) and (ii)]

∴∠A=∠D,∠B=∠E,∠C=∠F  

Thus ∆ABC ~∆DEF    [by AAA similarity criterion]

Hence proved

Related Topics 

1. Theorem 6.3

2. Theorem 6.5